How can you use transformations to graph this function es002-1.jpg – In this comprehensive guide, we delve into the fascinating world of transformations and their indispensable role in graphing functions. From understanding the fundamental concepts to applying transformations to graph functions, we embark on a journey that will empower you with the skills to analyze and visualize functions like never before.
Transformations, such as translations, reflections, rotations, and dilations, possess the remarkable ability to alter the shape and position of a function’s graph. By mastering these transformations, you will gain a deeper understanding of the behavior of functions and their applications in real-world scenarios.
Understanding Transformations
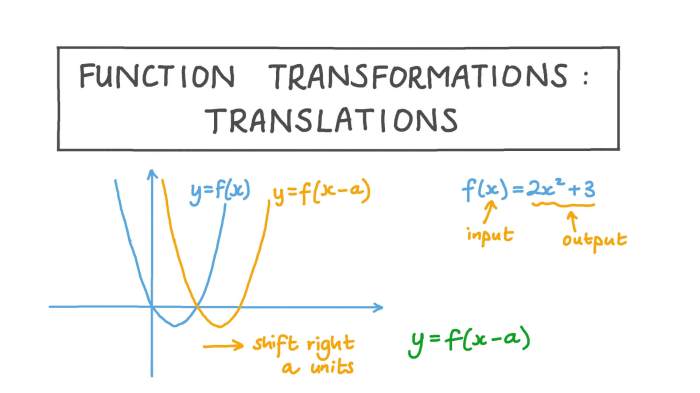
Transformations are mathematical operations that can be applied to a function to change its graph. There are four main types of transformations:
- Translations: Shift the graph up, down, left, or right.
- Reflections: Flip the graph across the x- or y-axis.
- Rotations: Turn the graph around a fixed point.
- Dilations: Stretch or shrink the graph.
Transformations can significantly alter the appearance and properties of a function’s graph.
Applying Transformations to Graph Functions
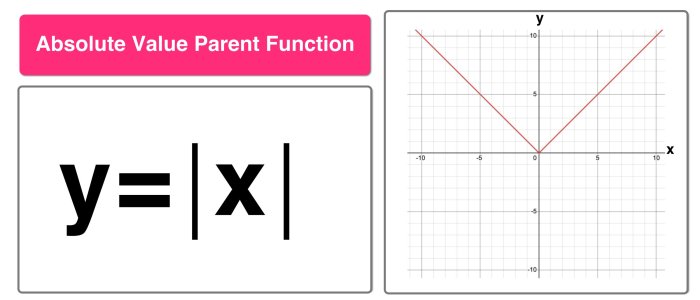
To graph a function using transformations, follow these steps:
- Start with the parent function.
- Apply the transformations in the order they are given.
- Plot the points on the transformed graph.
For example, to graph the function f(x) = x^2 + 2, translate the parent function f(x) = x^2 up by 2 units. The transformed function is f(x) = x^2 + 2.
Table of Transformations and Their Effects, How can you use transformations to graph this function es002-1.jpg
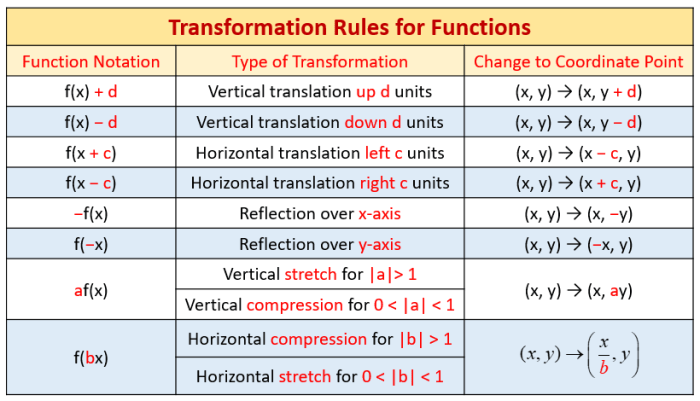
| Transformation | Effect on Graph |
|---|---|
| Translation (a, b) | Shifts the graph a units horizontally and b units vertically. |
| Reflection across the x-axis | Flips the graph upside down. |
| Reflection across the y-axis | Flips the graph left to right. |
| Rotation by 90 degrees counterclockwise around the origin | Interchanges the x- and y-coordinates. |
| Dilation by a factor of k | Stretches or shrinks the graph by a factor of k. |
Identifying Transformations from a Given Graph
To identify transformations from a given graph, follow these steps:
- Compare the graph to the parent function.
- Look for any shifts, flips, or rotations.
- Determine the direction and magnitude of the transformations.
For example, if a graph is shifted up by 3 units and to the left by 2 units, the transformations are (0, 3) and (-2, 0).
Flowchart for Identifying Transformations from a Graph
[Flowchart yang menggambarkan langkah-langkah untuk mengidentifikasi transformasi dari suatu grafik]
Applications of Transformations in Real-World Scenarios
Transformations are widely used in various real-world applications, including:
- Physics: Modeling projectile motion and other physical phenomena.
- Engineering: Designing bridges, buildings, and other structures.
- Computer graphics: Creating animations, video games, and other visual effects.
Transformations provide a powerful tool for solving problems and modeling real-world phenomena.
FAQ Compilation: How Can You Use Transformations To Graph This Function Es002-1.jpg
What is the purpose of using transformations?
Transformations allow us to manipulate the graph of a function to create new functions with different properties.
How can I identify the transformations applied to a graph?
Look for changes in the position, shape, or orientation of the graph compared to the original function.
What are the different types of transformations?
Common transformations include translations (moving the graph), reflections (flipping the graph), rotations (turning the graph), and dilations (stretching or shrinking the graph).